Ejemplo de problemas relacionados con la Segunda Ley de Newton.
- 1. Una fuerza le proporciona a la masa de 2,5 Kg. una aceleración de 1,2 m/s2. Calcular la magnitud de dicha fuerza en Newton y dinas.
Datos
m = 2,5 Kg.
a =1,2 m/s2.
F =? (N y dyn)
Solución
Nótese que los datos aparecen en un mismo sistema de unidades (M.K.S.)
Para calcular la fuerza usamos la ecuación de la segunda ley de Newton:
Como nos piden que lo expresemos en dinas, bastará con multiplicar por 105, luego:
- 2. ¿Qué aceleración adquirirá un cuerpo de 0,5 Kg. cuando sobre él actúa una fuerza de 200000 dinas?
Datos
a =?
m = 2,5 Kg.
F = 200000 dyn
Solución
La masa está dada en M.K.S., en cambio la fuerza está dada en c.g.s.
Para trabajar con M.K.S. debemos transformar la fuerza a la unida M.K.S. de esa magnitud (N)

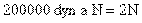
La ecuación de la segunda ley de Newton viene dada por:
- 3. Un cuerpo pesa en la tierra 60 Kp. ¿Cuál será a su peso en la luna, donde la gravedad es 1,6 m/s2?
Datos
PT= 60 Kp = 588 N
PL =?
gL = 1,6 m/s2
Solución
Para calcular el peso en la luna usamos la ecuación
Como no conocemos la masa, la calculamos por la ecuación: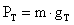 que al despejar m tenemos:
que al despejar m tenemos:
Esta masa es constante en cualquier parte, por lo que podemos usarla en la ecuación (I):

- 4. Un ascensor pesa 400 Kp. ¿Qué fuerza debe ejercer el cable hacia arriba para que suba con una aceleración de 5 m/s2? Suponiendo nulo el roce y la masa del ascensor es de 400 Kg.
Solución
Como puede verse en la figura 7, sobre el ascensor actúan dos fuerzas: la fuerza F de tracción del cable y la fuerza P del peso, dirigida hacia abajo.
La fuerza resultante que actúa sobre el ascensor es F – P
Aplicando la ecuación de la segunda ley de Newton tenemos:
Al transformar 400 Kp a N nos queda que:
400 Kp = 400 ( 9,8 N = 3920 N
Sustituyendo los valores de P, m y a se tiene:
F – 3920 N = 400 Kg. ( 0,5 m/s2
F – 3920 N = 200 N
Si despejamos F tenemos:
F = 200 N + 3920 N
F = 4120 N
- 5. Un carrito con su carga tiene una masa de 25 Kg. Cuando sobre él actúa, horizontalmente, una fuerza de 80 N adquiere una aceleración de 0,5 m/s2. ¿Qué magnitud tiene la fuerza de rozamiento Fr que se opone al avance del carrito?
Solución
En la figura 8 se muestran las condiciones del problema
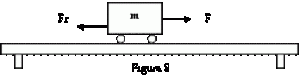
La fuerza F, que actúa hacia la derecha, es contrarrestada por la fuerza de roce Fr, que actúa hacia la izquierda. De esta forma se obtiene una resultante F – Fr que es la fuerza que produce el movimiento.
Si aplicamos la segunda ley de Newton se tiene:
Sustituyendo F, m y a por sus valores nos queda
80 N – Fr = 25 Kg. ( 0,5 m/s2
80 N – Fr = 12,5 N
Si despejamos Fr nos queda:
Fr = 80 N – 12,5 N
Fr = 67,5 N
IV. EJERCICIOS DE MOMENTO DE INERCIA
El momento de inercia es una medida de la inercia rotacional de un cuerpo. Cuando un cuerpo gira en torno a uno de los ejes principales de inercia, la inercia rotacional puede ser representada como una magnitud escalar llamada momento de inercia. Sin embargo, en el caso más general posible la inercia rotacional debe representarse por medio de un conjunto de momentos de inercia y componentes que forman el llamado tensor de inercia. La descripción tensorial es necesaria para el análisis de sistemas complejos, como por ejemplo en movimientos giroscópicos.
El momento de inercia refleja la distribución de masa de un cuerpo o de un sistema de partículas en rotación, respecto a un eje de giro. El momento de inercia sólo depende de la geometría del cuerpo y de la posición del eje de giro; pero no depende de las fuerzas que intervienen en el movimiento. Velocidad constante del bloque v=0.08 m/s
Tensión de la cuerda, es el peso del bloque, F=2000·9.8=19600 kg
Momento, M=F·r=19600·0.3=5880 N·m
Velocidad angular, ω=v/r=0.08/0.3=4/15 rad/s
Potencia, P=M·ω=5880·4/15=1568 W
Trabajo, W=M·θ=P·t=1568·10=15680 J Solución 1: III. EJERCICIOS DE DINAMICA ROTACIONAL
Es una parte de la mecánica que estudia a los sólidos su traslación y su rotación. PROBLEMA Nº 4 ¿Cuál será la fuerza aplicada a un cuerpo que pesa 12800 N si lo hace detener en 35 s?, la velocidad en el instante de aplicar la fuerza era de 80 km/h.
Solución 4:
Primero, empleando ecuaciones de cinemática, calculamos la aceleración (negativa) producida por la fuerza.
v2 - v1 = a.t
a = - v1/t
a = (- 22,22 m/s)/35 s
a = -0,635 m/s ²
La masa resulta:
P = m.g
m = P/a
m = 12800 N/(10 m/s ²)
m = 1280 kg
Luego:
F = m.a
F = 1280 kg.(-0,635 m/s ²)
F = -812,7 N La fuerza es contraria al movimiento. a)F = m.a
m = F/a
m = 50 N/1,5 m/s ²
m = 33,33 kg
b) Como parte del reposo:
v = a.t
v = (1,5 m/s ²).10 s
v = 15 m/s
c)e = ½.a.t ²
e = ½.(1,5 m/s ²).(10 s) ²
e = 75 m Sobre un cuerpo actúa una fuerza constante de 50 N mediante la cual adquiere una aceleración de 1,5 m/s ², determinar:
a) La masa del cuerpo.
b) Su velocidad a los 10 s.
c) La distancia recorrida en ese tiempo.
Solución: PROBLEMA Nº 2 Solución 1:
a) La masa la hallamos mediante la fórmula de densidad.
δ = m/V
m = δ.V
m = (7,8 g/cm ³).(32 cm ².20 cm)
m = 4992 g
m = 5 kg
b)F = m.a
a = F/m
a = 100 N/5 kg
a = 20 m/s ²
c) Suponiendo que parte del reposo.
e = v1.t + ½.a.t ²
e = ½.a.t ²
e = ½.(20 m/s ²).(30 s) ²
e = 9000 m Sea un paralelepípedo rectángulo de hierro (δ = 7,8 g/cm ³) cuya base es de 32 cm ² y su altura es de 20 cm, determinar:
a) La masa.
b) La aceleración que le provocará una fuerza constante de 100 N.
c) La distancia recorrida durante 30 s.
Datos:
b = 32 cm ²
h = 20 cm
δ = 7,8 g/cm ³
F = 100 N
t = 30 s PROBLEMA Nº 1 II. EJERCICIOS DE DINAMICA
La dinámica es la parte de la física que describe la evolución en el tiempo de un sistema físico en relación con las causas que provocan los cambios de estado físico y/o estado de movimiento. El objetivo de la dinámica es describir los factores capaces de producir alteraciones de un sistema físico, cuantificarlos y plantear ecuaciones de movimiento o ecuaciones de evolución para dicho sistema de operación.
PROBLEMA 3: Un cubo de madera de 2 kg y 20 cm de arista, que descansa sobre una superficie horizontal sin fricción, está sujeto a una barra rígida de longitud 2 m y masa 300 g fijada a la superficie por un extremo en el punto O y por el otro al centro del cubo.
Una bala de masa 50 g y velocidad 200 m/s se incrusta en el cubo a la altura de su centro de masa (en la dirección que forma 30º con la perpendicular al cubo ) ¿Cuál es la velocidad angular del sistema después del choque. Momentos de inercia respecto de un eje que pasa por el cm del cubo: I=ma2/6 y de la varilla I=mL2/12 ¿Cuál es la velocidad angular del sistema después del choque?.
¿Qué principio físico has aplicado?. ¿por qué? ¿Se conserva la energía en esta colisión?.
Momentos de inercia respecto de un eje que pasa por el cm del cubo:
y de la varilla
PROBLEMA 2: Un cubo de madera de 2 kg y 20 cm de arista, que descansa sobre una superficie horizontal sin fricción, está sujeto a una barra rígida de longitud 2 m y masa 300 g fijada a la superficie por un extremo en el punto O y por el otro al centro del cubo. Una bala de masa 50 g y velocidad 200m/s se incrusta en el cubo a la altura de su centro de masa (en la dirección perpendicular al cubo, tal como se muestra en la figura) la velocidad angular de rotación cuando los centros de las esferas se
encuentran en los extremos de la varilla. Qué principio físico aplicas?. Por qué?.
b) Hallar la energía cinética del sistema en los dos casos.
Dato momento de inercia de una esfera y de la varilla I. EJERCICIOS DE CHOQUE
PROBLEMA 1: Ivan Cruz Guerra Ihuaraqui
Código: 1210980 PROBLEMAS RESUELTOS
FISICA El yoyo de la figura se desenrolla por acción de la tensión T apoyado en una superficie plana. Hallar una expresión para la aceleración angular del yoyo. Solución 2: PROBLEMA Nº 3
Un bloque de 2000 kg está suspendido en el aire por un cable de acero que pasa por una polea y acaba en un torno motorizado. El bloque asciende con velocidad constante de 8 cm/s. El radio del tambor del torno es de 30 cm y la masa de la polea es despreciable.
¿Cuánto vale el momento que ejerce el cable sobre el
tambor del torno?
¿Cuánto vale la velocidad angular del tambor del torno?
¿Qué potencia tiene que desarrollar el motor?.Calcular el
trabajo realizado durante 10 s PROBLEMA Nº 1 PROBLEMA Nº 5 Un cuerpo posee una velocidad de 20 cm/s y actúa sobre él una fuerza de 120 N que después de 5 s le hace adquirir una velocidad de 8 cm/s. ¿Cuál es la masa del cuerpo?.
Solución 5:
De acuerdo a los datos la fuerza le produce a la masa una desaceleración.
Primero, empleando ecuaciones de cinemática, calculamos la aceleración (negativa) producida por la fuerza.
v2 - v1 = a.t
a = (v2 - v1)/t
a = (0,08 m/s - 0,2 m/s)/5 s
a = -0,024 m/s ²
Luego:
F = m.a
m = F/a
m = -120 N/(-0,024 m/s ²)
m = 5000 kg
PROBLEMA Nº 3 Cuál será la intensidad de una fuerza constante al actuar sobre un cuerpo que pesa 50 N si después de 10 s ha recorrido 300 m?.
Solución 3:
Primero calculamos la aceleración:
e = ½.a.t ² a = 2.e/t ²
a = 2.300 m/(10 s) ² a = 6 m/s ²
Ahora calculamos la masa del cuerpo:
P = m.g m = P/g
m = 50 N/(10 m/s ²) m = 5 kg
Con estos datos calculamos la fuerza:
F = m.a
F = 5 kg.6 m/s ² F = 30 N
Determina la velocidad angular de un disco de 1kg de masa y radio 20cm que rota con eje en su centro de masa con una energía cinética de 800J
Solución 1: Solución 2: Solución 3: Solución 2: PROBLEMA Nº 1 Determinar la velocidad angular de un disco de 1 kg de
masa y radio 20 cm que rota con eje en su centro de
masa con una energía cinética de 800 J.




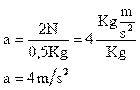

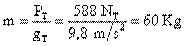
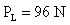


No hay comentarios:
Publicar un comentario